Таинственный бокал похож на крюк
Вокруг него рассыпаны алмазы
Не целовался я с тобой ни разу
Мой омерзительный, безногий друг
Но, скорее, это человеческое воображение способно приписать смысл любому тексту, написанному без ошибок — пусть и бессмысленному изначально. (Мой омерзительный безногий друг — бюст В.И.Ленина.) Как рисунки в пейзажных агатах.
Мне, кстати, в магистратуре мехмата МГУ пришлось вести курс по классическому машинному обучению (всё, что было до нейросетей). Это совсем не моя тематика, поэтому новая для меня, и, надо сказать, от некоторых алгоритмов я был в полном восторге (век живи, век учись) — например, ядровый метод опорных векторов. Теорему Куна-Таккера, на которой он основан, мы проходили в курсе функционального анализа (или оптимального управления) на мехмате где-то в конце 70-х годов, и вот уж я никак не ожидал, что она мне понадобится через 40 лет! (Теперь ее называют теоремой Карруша-Куна-Таккера.) Можно почитать про всё это на моей страничке. Пришлось написать много программ на Питоне для графических иллюстраций разных методов. Самое последнее: рассказ про решающие деревья (цель всего был градиентный бустинг, один из самых сильных классических методов машинного обучения наряду с ядровым методом опорных векторов), вот разные забавные картинки оттуда:
Построение классификатора на основе решающего дерева
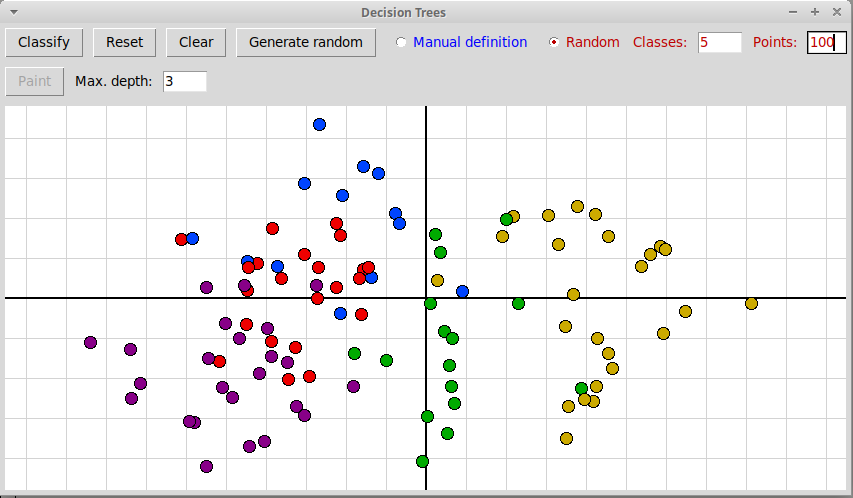
Исходные объекты (обучающая база данных):
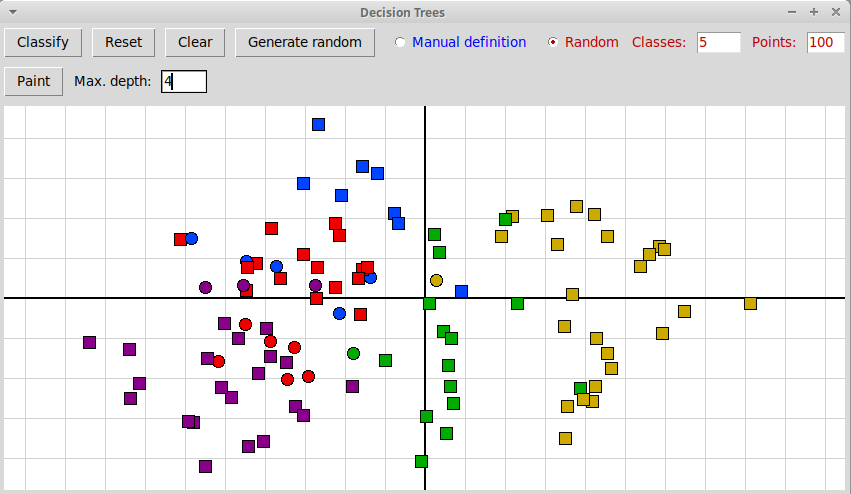
После классификации (максимальная глубина дерева 4):
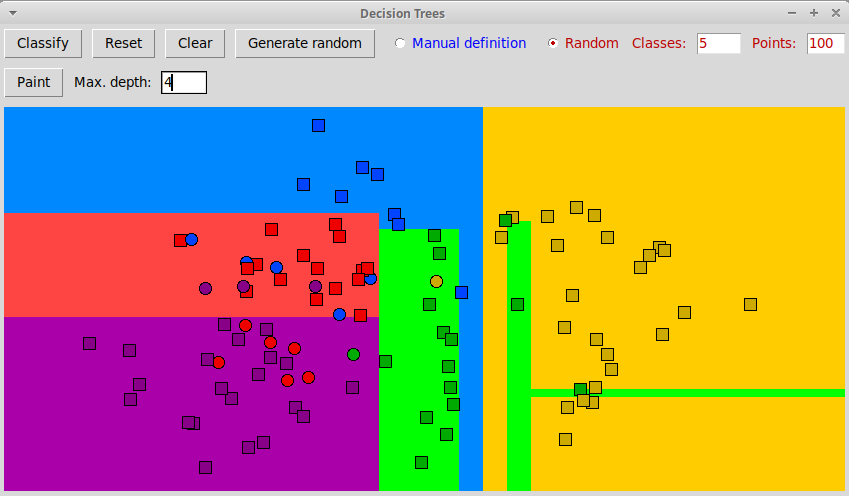
И прогноз для произвольных объектов:
(Исходный код основной программы на Питоне decisionTrees.py, архив всех необходимых файлов decisionTrees.zip)
В задаче регрессии с применением решающих деревьев довольно забавным получается представление изображения с помощью решающего дерева. Вот исходная картинка, здание МГУ:
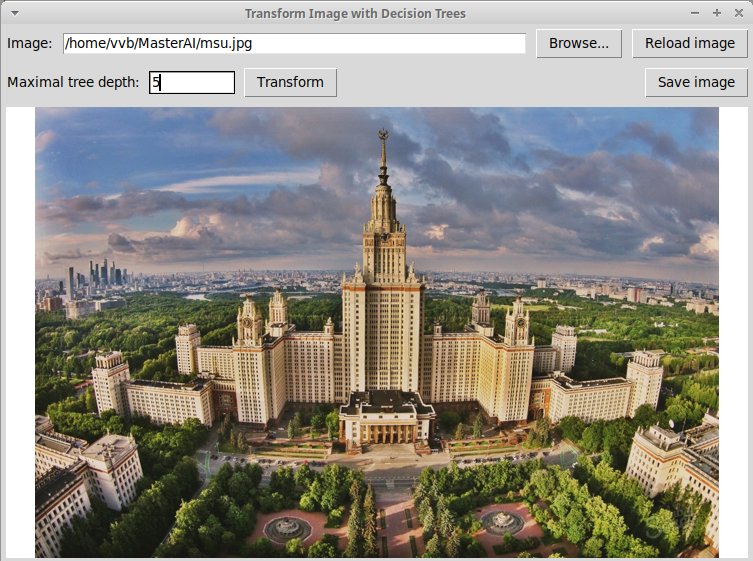
Применение решающего дерева глубины 10 в задаче регрессии дает вот такую картинку:
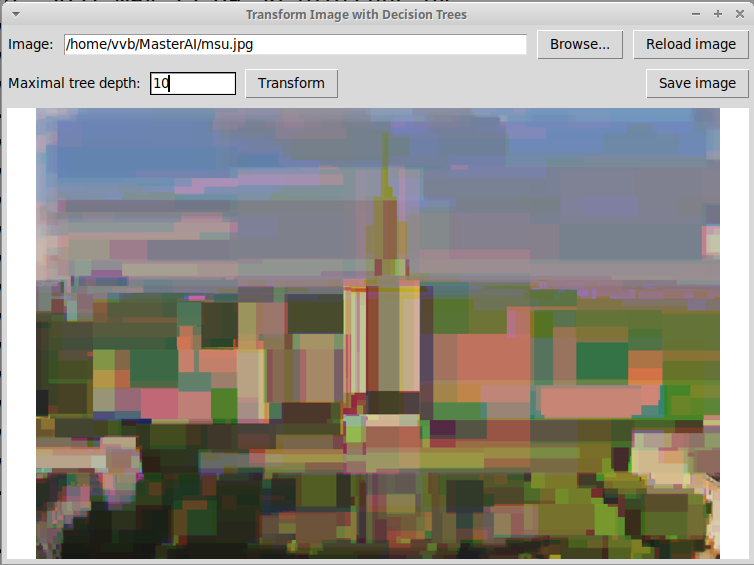
Дерево глубины 15:
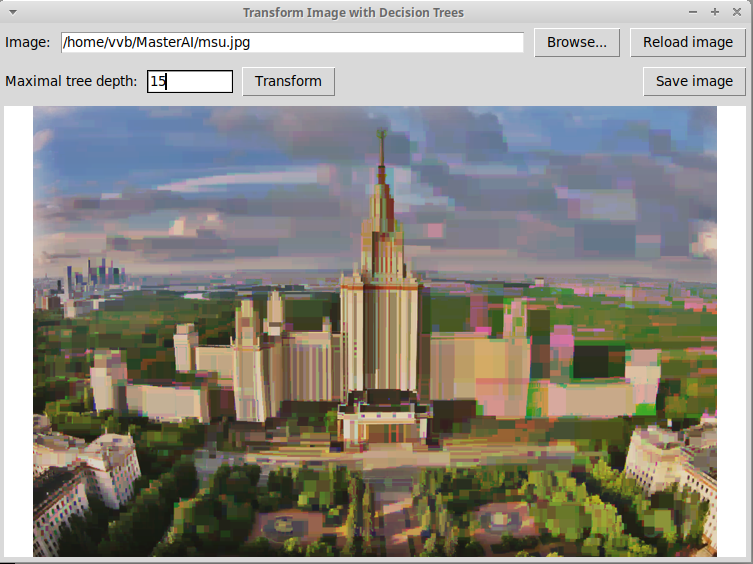
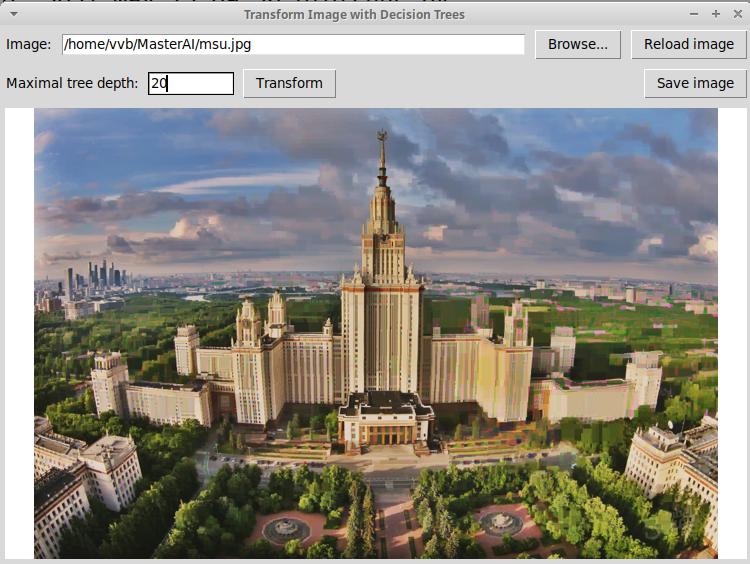
Дерево глубины 20 дает уже почти что исходное изображение:
Исходный код программы на Питоне: imageRegrTrees.py
(Деревья очень легко переобучаются, но в данном примере это неважно, потому что нам не надо строить математическую модель, способную предсказывать. Но в градиентном бустинге такие глубокие деревья не используются, поскольку они переобучаются, там используется ансамбль деревьев небольшой глубины, зато деревьев много — по умолчанию до 100, каждое следующее дерево исправляет ошибки ансамбля предыдущих деревьев.)
