 К основным движениям следует отнести скольжение, вращательные движения звеньев тела и отталкивание. К основным движениям следует отнести скольжение, вращательные движения звеньев тела и отталкивание.
СКОЛЬЖЕНИЕ
Движения тела фигуриста при скольжении по дуге характеризуются большим количеством величин, таких, как скорость, ускорение, радиус кривизны дуги скольжения, сила инерции, сила давления конька на лед, сила трения. Для того чтобы определить, как связаны эти величины, рассмотрим схему одноопорного скольжения (рис. 9).
На тело фигуриста, скользящего по дуге окружности радиуса q, имеющего в данный момент скорость V, действуют: сила веса Р, сила трения F, направленная в сторону, противоположную движению; касательная сила инерции Uf параллельная оси ох и направленная противоположно замедлению; нормальная или центробежная сила инерции /ш параллельная оси оу; опорная реакция N, равная давлению фигуриста на лед и направленная по продольной оси вверх.
В рассматриваемый момент времени тело фигуриста находится в координатной плоскости xyz с наклоном продольной оси на угол а к вертикали; / — расстояние от о. ц. т. до точки опоры О.
Составим уравнения равновесия сил и моментов, для чего спроектируем все силы на координатные оси, и составим уравнения моментов этих сил относительно осей координат:
Наибольший интерес представляют четыре первых уравнения. Подставляя вместо сил инерции и силы трения их выражения, получим: *
 Рассмотрим ряд практических выводов, которые можно сделать, анализируя приведенные уравнения.
Важной характеристикой скольжения является наклон продольной оси тела к поверхности льда. Этот наклон тесно связан с обеспечением реберности скольжения — одного из основных условий качественного выполнения фигуры.
Преобразуя уравнение (4), получаем
где р — радиус кривизны следа.
В формулу не входит масса тела. Отсюда первый важный вывод:
угол наклона продольной оси тела фигуриста зависит только от величины радиуса дуги и скорости скольжения, но не зависит от массы, а следовательно, и от веса фигуриста.
Другими словами, легкая фигуристка и тяжелый по весу фигурист при скольжении по дуге одинакового радиуса с одной и той же скоростью имеют один и тот же угол наклона продольной оси.
Из формулы (5) можно сделать другой вывод:
угол наклона продольной оси увеличивается пропорционально квадрату скорости скольжения и уменьшается с увеличением радиуса дуги скольжения.
Подсчитаем угол отклонения продольной оси тела от вертикали для фигуриста, который после отталкивания начал скользить по дуге окружности радиуса (р) 3 м, имея скорость (V) 2,4 м в 1 сек:
откуда а= 11°5'.
При скольжении с меньшей скоростью угол наклона меньше. Известно, что при малых углах наклона конек опорной ноги, может оставить на льду двуреберный след, а это грубая ошибка.
Формула (5) связывает между собой четыре величины. Следовательно, каждую из этих величин можно выразить через остальные. Например, скорость скольжения (V) будет равна:


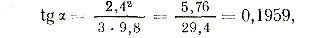

Иными словами, мы получим выражение, из которого видно, что причиной увеличения давления конька на лед является нормальная (центробежная) сила инерции, появляющаяся при скольжении по кривой.
Одной из проблем выполнения обязательных фигур, особенно в форме восьмерок, является сохранение такой величины скорости скольжения, которая обеспечивает ре-берность скольжения и качество поворотов на протяжении выполнения всей фигуры.
Рассмотрим причины, вызывающие замедление скольжения. Условимся, что в это время фигурист не выполняет поворотов и перетяжек, а также не сгибает и не разгибает опорную ногу.
Основной тормозящей силой при скольжении в обязательных фигурах является сила трения (сопротивление воздуха при малых скоростях незначительно).
Определим связь величины замедления с коэффициентом трения конька о лед. Из равенства (1) можно определить замедление wT при одноопорном скольжении:
Как видим, при одноопорном скольжении замедление прямо пропорционально давлению на лед, коэффициенту трения и обратно пропорционально массе тела.
Для определения численного значения замедления в ряде случаев удобно воспользоваться другим видом формулы (10). После преобразования ее мы получаем:
Из формулы (11) видно, что при одноопорном скольжении замедление прямо пропорционально коэффициенту трения конька о лед и обратно пропорционально косинусу угла наклона продольной оси тела фигуриста.
Поскольку на практике величина cosce меняется незначительно, а ускорение силы тяжести g — величина постоянная для данного места, то замедление зависит главным образом от коэффициента трения конька опорной ноги о лед.
Коэффициент трения скольжения зависит от многих причин: от качества льда, его температуры и состава воды, от материала лезвия конька и его заточки. Чем ниже температура льда, тем больше коэффициент трения. На качество льда влияет количество минеральных солей, растворенных в воде. Лед, полученный из жесткой воды, создает большее сопротивление скольжению, чем лед из мягкой воды. При низкой температуре лед тверже, а при повышенной мягче. В первом случае скольжение затрудняется из-за твердости льда, а во втором — тем, что лезвие конька врезается в мягкий лед.
Коэффициент трения на хорошем льду минимален, что уменьшает величину замедления при скольжении, Вели»
Из этой же формулы (5) можно определить выражение для радиуса кривизны дуги скольжения:
При изучении техники обязательных фигур важно знать силы взаимодействия конька со льдом.
Равенство (3) позволяет определить величину давления конька опорной ноги на лед, равную

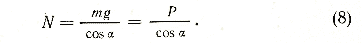
Так как косинус угла а всегда меньше единицы, то из формулы (8) следует важный вывод:
при скольжении по дуге давление конька на лед всегда больше веса фигуриста и становится равным ему при скольжении по прямой.
Для более детального анализа зависимости величины давления конька на лед воспользуемся уравнением (2):

Как видим, давление на лед зависит от массы тела фигуриста, квадрата скорости, радиуса кривизны дуги скольжения и синуса угла наклона продольной оси тела фигуриста. Давление возрастает с увеличением массы тела фигуриста и скорости его скольжения и убывает с увеличением радиуса кривизны дуги и угла наклона продольной оси тела. При а=90°, т. е. когда ось расположена горизонтально, sina = l, тогда формула (9) принимает вид:



Величина коэффициента трения стали о лед колеблется в пределах 0,01—0,03.
Подсчеты показывают, что при выполнении круга вперед-наружу средние величины скорости на каждой четверти окружности равняются: V, = 2,2 м/сек, V2 = = 1,87 м/сек, Уз = = 1,55 м/сек, У4 = 1,34 м/сек.
На рис. 10 приведен график уменьшения скорости скольжения при выполнении круга вперед-наружу. Как видим, характер уменьшения скорости соответствует равнозамедленному движению.
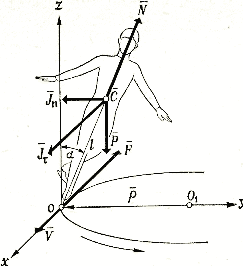 Рис. 9. Силы, действующие на тело фигуриста при скольжении
Другими словами, у квалифицированных фигуристов замедление при простом скольжении по дугам практически постоянно.
ВРАЩАТЕЛЬНЫЕ ДВИЖЕНИЯ
При выполнении обязательных фигур тело участвует во вращательных движениях. В специальной литературе сложное движение тела фигуриста при скольжении по дуге принято делить на поступательное и вращательное. Из-за такого неточного разделения выпадала из виду одна из важных особенностей движения, имеющая принципиальное значение для изучения техники поворотов в обязательных фигурах.
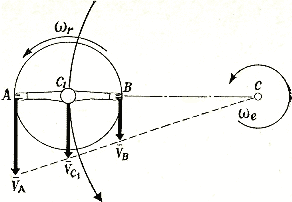 Рис. 11. Схема движения тела при скольжении по окружности
Итак, рассмотрим схему движения фигуриста при скольжении по дуге окружности.
На рис. 11 приведено схематическое изображение (вид сверху) такого скольжения. Отчетливо видно, что во время скольжения по окружности тело фигуриста вращается вокруг оси, проходящей через центр окружности. Так, при выполнении одного круга опорная нога и ее конек совершают один оборот, т. е. поворот на 360°. Другими словами, тело его участвует во вращательном движении, а не в поступательном.
Видно также, что точки тела, расположенные на разном расстоянии от центра окружности, имеют разные величины скоростей. Это еще раз подчеркивает, что нельзя говорить о поступательном движении тела фигуриста при скольжении по дуге — известно, что при поступательном движении скорости всех точек тела в данный момент одинаковы.
Итак, скольжение фигуриста по окружности — есть движение вращательное.
Движение при скольжении по дуге может быть еще более сложным. Рассмотрим случай, в котором при скольжении по дуге фигурист начинает вращаться также вокруг своей продольной оси (рис. 12). В этом случае тело его одновременно вращается вокруг оси, проходящей через центр окружности, и вокруг своей продольной оси. Обозначим угловые скорости этих вращений ые и шг, где
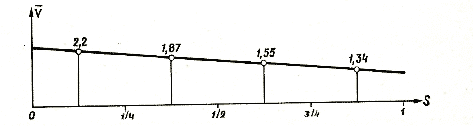 Рис. 10. Уменьшение скорости скольжения при выполнении круга вперед-наружу
 Рис. 12. Сложение вращений при скольжении по окружности и повороте вокруг продольной оси:
/7 — ось поворота (ось тела); В — ось, проходящая через центр круга;
М — ось мгновенного вращения; а — направления вращений совпадают;
б — направления вращений противоположны
юе — угловая скорость тела при скольжении по дуге,
Юг — угловая скорость в повороте тела вокруг своей продольной оси.
Случай такого сложного движения, когда фигурист одновременно участвует в двух вращательных движениях, в механике называется сложением вращений.
В нашем случае оси слагаемых вращений будем считать параллельными, так как при малых скоростях скольжения по дуге окружности наклон продольной оси небольшой — 4—5°. Такое допущение возможно, так как картина сложения вращений, в сущности, не изменится и в том случае, если одна из осей имеет некоторый наклон.
Известно, что при сложении двух вращений вокруг параллельных осей возникает результирующее мгновенное вращательное движение вокруг оси, параллельной осям слагаемых вращений. Другими словами, при наличии вращений тело фигуриста в тот момент будет вращаться вокруг оси мгновенного вращения, не совпадающей с осями слагаемых вращений. Правило нахождения величины угловой скорости мгновенного вращения и местоположения его оси аналогично правилу определения величины и места приложения результирующей силы при сложении параллельных сил. Если оба вращения направлены в одну сторону, то угловая скорость результирующего вращения вокруг мгновенной оси равна сумме угловых скоростей поворота и скольжения по дуге: со = сог + «е. Мгновенная ось вращения находится на прямой, соединяющей оси, и делит эту прямую на отрезки, величины которых обратно пропорциональны величинам слагаемых скорости. Если оба вращения направлены в разные стороны, то угловая скорость результирующего вращения равна разности угловых скоростей поворота и скольжения по дуге: со = сог — сое. Ось мгновенного вращения расположена вне окружности скольжения.
На практике эта закономерность проявляется следующим образом. Если фигурист при скольжении по дуге попытается придать своему телу вращение вокруг продольной оси, то оно немедленно начнет вращаться вокруг оси мгновенного вращения, не совпадающей с продольной осью тела. Когда оба вращения совершаются в одну сторону, то ось мгновенного вращения сдвигается в сторону центра окружности скольжения и кривизна увеличивается; когда направления вращений противоположны, то ось мгновенного вращения находится вне окружности скольжения; сначала уменьшается кривизна дуги, а затем меняется направление скольжения.
Смещение оси мгновенного вращения имеет большое практическое значение для обеспечения точности начертания поворотов и дуг. О том, как учитывать это явление при обучении обязательным фигурам, разговор пойдет дальше.
Положение оси мгновенного вращения может быть определено следующим образом. Фигурист за 13 сек. описывает окружность радиусом 3 м, совершает поворот вокруг продольной оси тела на 180° за 0,3 сек. Вращения направлены в одну сторону. В этом случае
 откуда
 Следовательно, ось вращения сдвинута в сторону центра описываемой окружности от продольной оси тела, вокруг которой совершался поворот, на 13 см. Таким же образом можно подсчитать, что если оба вращения направлены в разные стороны, то мгновенная ось вращения будет находиться вне окружности на расстоянии около 13 см. Трение конька не учитывается.
Рассматривая изложенное с точки зрения начертания обязательных фигур, следует отметить, что попытка придать телу вращение вокруг продольной оси приводит к искривлению следа внутрь, если вращение происходит в положительном направлении, и наружу, если направление отрицательное.
Значительную часть элементов обязательных фигур составляют повороты. Замечено, что в основе выполнения поворотов лежат вращательные движения. Здесь очень важно правильно понимать причины, вызывающие поворот. Получить представление о механизме вращательного компонента выполнения поворотов можно, используя описанное правило сложения вращения вокруг параллельных осей и закон сохранения кинетического момента.
Рассмотрим, можно ли выполнить поворот, приближая к продольной оси и удаляя от нее звенья тела, т. е. с помощью изменения момента инерции тела относительно продольной оси. Напомним: если тело в целом не имеет начального вращения вокруг своей продольной оси, то ни приближения, ни удаления звеньев не могут вызвать вращения.
Итак, рассмотрим возможность выполнения поворотов с помощью приближения и удаления звеньев тела. Случай 1. Фигурист, пытаясь сделать поворот, одним из способов (при толчке или скольжении по дуге) сообщает своему телу вращение в положительном направлении. Тело начнет вращаться вокруг оси мгновенного вращения, расположенной внутри окружности. Кривая скольжения будет закругляться. В момент группировки рук и Свободной ноги резко увеличивается скорость вращения тела в положительном направлении. Плечевой пояс, таз, опорная нога, ее конек начинают поворачиваться. Для замедления вращения фигурист разгруппировывается, скорость вращения тела падает, в результате дальнейшее скольжение конька происходит по более пологой дуге. Однако тело продолжает вращаться в направлении, которое получено при толчке.
Приведенная схема движения приближенно соответствует схеме выполнения тройки и показывает принципиальную возможность выполнения тройки изменением момента инерции тела фигуриста относительно продольной оси.
Другим поворотом, подготовка к которому осуществляется в положительном направлении, является крюк. Сразу же необходимо отметить, что на основе схемы, описанной раньше, выполнение крюка принципиально невозможно. Доказать это просто. Приближение и удаление звеньев тела может изменить лишь величину скорости вращения тела, но не его направление. В крюках направление скольжения конька до и после поворота противоположно.
Сказанное может быть подтверждено практическими попытками выполнить таким способом крюк на льду. Сообщив своему телу общее вращение в положительном направлении, фигурист, приближая руки к продольной оси тела и стремясь выполнить крюк, будет выполнять поворот тройкой.
Случай 2. Фигурист, скользя по дуге, вращением верхней части тела сообщил всему телу вращение в отрицательном направлении. Вследствие сложения двух вращений, направленных в разные стороны (вокруг центра фигуры и вокруг своей продольной оси), ось мгновенного вращения тела смещается наружу круга, дуга постепенно уплощается. Группируя руки и свободную ногу, фигурист увеличивает скорость вращения тела в отрицательном направлении. Плечевой пояс, туловище, таз увлекают во вращение опорную ногу, возникает поворот в сторону общего вращения тела. Затем выполняется разгрупиировка и как следствие переход к скольжению по более пологой дуге.
При этом, естественно, сохраняется общее вращение тела в направлении поворота, а скольжение происходит в направлении, совпадающем с направлением вращения тела, полученного до поворота.
Такая схема поворота соответствует выкрюку, и, подобно повороту тройкой, показывает принципиальную возможность выполнения поворота выкрюком с помощью приближения звеньев тела к оси вращения.
Описанная схема движения показывает также, что поворот скобкой не может быть выполнен этим способом, так как в скобке направление скольжения при завершении должно быть противоположно направлению общего вращения тела, полученного перед поворотом. А как мы уже говорили, изменение момента инерции тела не может изменить направление его поворота. Принципиальную невозможность выполнить поворот скобкой приближением звеньев тела к продольной оси тела и удалением от нее можно убедительно доказать также на практике.
Таким образом, утверждения о том, что механизм вращательного компонента поворота заключается в изменении угловой скорости вращения тела с помощью изменения момента инерции для скобок и крюков, принципиально неверны. Другими словами, ни скобку, ни крюк, невозможно выполнить, приближая руки и свободную ногу к продольной оси тела или удаляя от нее.
Мы уже говорили, что существует принципиальная возможность выполнить повороты тройкой и выкрюком с помощью группировки рук и свободной ноги, предварительно сообщив телу начальное вращение. Реальная попытка нарисовать на льду фигуру с тройками, например любую фигуру в форме восьмерки или крюк, используя этот способ выполнения поворотов, окажется безрезультатной. Дело в том, что, если при скольжении по окружности тело фигуриста имеет общее вращение в сторону закривления дуги или в противоположную, это приведет к смещению мгновенной оси вращения, т. е. к искривлению дуги выезда из поворота внутрь или наружу.
Таким образом, практически техника выполнения любых поворотов путем изменения момента инерции тела относительно продольной оси является неприемлемой для обязательных фигур.
МЕХАНИКА ПОВОРОТОВ
Для того чтобы иметь правильное представление о механической сущности поворотов, целесообразно анализ этих движений проводить на основе закона сохранения кинетического момента. В данном случае имеется в виду, что если на тело не действуют внешние силы, то вращение какого-либо звена в одном направлении вызывает поворот остальной части тела в противоположном. Количественно скорости этих встречных вращений обратно пропорциональны моментам инерции звеньев. Аналогичная зависимость существует и между углами поворота звеньев: поворот звена с малым моментом инерции (например, руки) на большой угол вызывает поворот на небольшой угол звена с большим моментом инерции (остальной части тела). Эту закономерность важно учитывать в технике поворотов.
Для упрощения картины исследуемого движения при предварительном рассмотрении пренебрежем внешними силами. Будем считать, что момент сил сопротивления, возникающий между коньком опорной ноги и льдом, равен нулю, т. е. силы сопротивления отсутствуют. На практике фигуристы высокого класса часто выполняют повороты так, что след, остающийся на льду, бывает исключительно тонким, как говорят, волосяным. Совершенно очевидно, что в таких случаях величины моментов сил вращательного взаимодействия конька со льдом очень незначительны.
При начале разрешения плечевой пояс выполняет так называемое обратное движение, т. е. поворот плечевого пояса и рук относительно таза. В силу закона сохранения кинетического момента это движение одновременно вызывает вращение нижней части тела в противоположном направлении. Важно отметить, что при правильном выполнении поворота во время обратного движения выполняется и въезд в вершину элемента и выезд из него. В практике часто встречается ошибочное мнение о том, что обратному движению соответствует только выезд из вершины поворота.
Итак, поворот верхней части тела в одном направлении вызывает поворот нижней части в другом направлении. Тогда кинетический момент поворота верхней части тела должен быть равен кинетическому моменту нижней части тела: Кн = Кв-
Поскольку направления поворота верхней и нижней частей тела противоположны, получаем: Кн — Кв = 0\ /ншн—/вшв = 0. Это значит, что вращение верхней части тела уравновешено вращением нижней его части таким образом, что общее вращение тела отсутствует и его суммарный кинетический момент равен нулю.
Для получения более точной механической картины поворота несложно учесть влияние моментов сил сопротивления, возникающих между коньком и льдом. Очевидно, что моменты сил сопротивления направлены навстречу повороту конька, т. е. навстречу вращению нижней части тела. В результате силы сопротивления будут ослаблять вращение нижней части, говоря точнее—■ уменьшать кинетический момент нижней части тела. При больших силах сопротивления, возникающих между коньком и опорой, например при стоянии на резиновом коврике, поворот верхней части тела может не вызвать поворота нижней части с коньком.
Условно обозначим потери кинетического момента в результате сил взаимодействия конька со льдом через Кп. Учитывая, что силы сопротивления направлены навстречу повороту нижней части тела с коньками, можно написать: Ка—/СЕ—^Сп = 0.
Полученное соотношение является своего рода формулой поворота. Она позволяет проанализировать возможные искажения рисунка поворота в результате несбалансированного вращения нижней и верхней частей тела.
Случай 1. Кинетический момент нижней части больше суммы кинетического момента верхней части и кинетического момента потерь Кн> Кв + Кп-
Практически это означает, что в результате разрешения вращение нижней части преобладает над противоположным ему вращением верхней части. В таком случае после поворота тело приобретает общее вращение в направлении, в котором вращалась опорная нога в повороте. Появление остаточного вращения тела в этом направлении вызывает характерный «перекрученный» рисунок поворота (рис. 13, а).
Случай 2. Кн-<Кв + Кп- Кинетический момент нижней части меньше суммы кинетического момента верхней части и кинетического момента потерь. В этом случае фигурист ощущает, что в результате разрешения обратное движение, т. е. вращение плечевого пояса и рук, увлекло в поворот все тело. Это «останавливающее» вращение приводит к так называемой недокрученной форме поворота (рис. 13, б).
Искажение формы поворота тесно связано со смещением мгновенной оси вращения и обусловлено им. В случае Кн~>Кв + Кп, т. е. вращение тела в сторону вращения нижней части тела, мгновенная ось вращения смещается за пределы окружности и вызывает нарушение равновесия и соответствующее искажение следа (как показано на рис. 13, а).
В случае К<Кв + + Кп мгновенная ось находится внутри круга и вызывает нарушение равновесия в ту же сторону и соответствующее искажение рисунка (см. рис. 13,6).
Итак, наличие общего вращения тела после поворота вызывает смещение мгновенной оси вращения, а в результате — нарушение равновесия и искажение рисунка по правилу, приведенному в начале раздела.
Поскольку при выполнении поворотов звенья тела фигуриста совершают вращательные движения, представляют интерес особенности геометрии отдельных фигур. Ведь при выполнении поворотов участок конька, соприкасающийся со льдом, в точности повторяет контур фигуры.
Одной из кинематических характеристик движения является так называемая центроида. Центроидой называют геометрическое место точек мгновенных центров скоростей тела, т. е. точек, через которые проходят оси мгновенного вращения. На рис. 14 приведены центроиды движения конька при поворотах тройкой, скобкой, крюком, выкрюком и для фигуры с петлей.
 Рис. 13. Искажение формы поворота: а — перекрученная; б — недокрученная
Несмотря на то что центроида — это кривая, по которой перемещается не реальное тело, а воображаемая точка, форма ее в некоторой степени отражает геометрическую сложность траектории движения тела. Именно поэтому можно сделать предположение, что форма центроиды в каждом повороте — в тройках, скобках, крюках и вы-крюках отражает сложность выполнения элемента. Так, на рис. 14 видно, что в тройке центроида имеет форму плавной замкнутой кривой, расположенной внутри окружности. Она не имеет разрывов. Это говорит о том, что конек при скольжении не меняет направления вращения. В крюке ось мгновенного вращения конька последовательно проходит через точки 1, 2, 3, в точке 3 уходит в бесконечность и затем переходит в точку 4 — центр второго круга. В данном случае перемещение оси мгновенного вращения конька более сложно. Особую сложность имеет изменение направления вращения конька в конце выезда из поворота. Смена направления вращения конька в этой точке на практике часто сопровождается искажениями следа. Наиболее распространенное из них — поздняя смена направления скольжения с характерной S-образной формой следа.
Аналогичная форма центроиды и в выкрюке. Разница лишь в том, что смена направления вращения конька происходит до поворота. Кривая центроиды в этой точке имеет разрыв, и именно в этом месте фигуры наиболее часто встречаются искажения следа. Как правило, это S-образная форма подъезда к повороту.
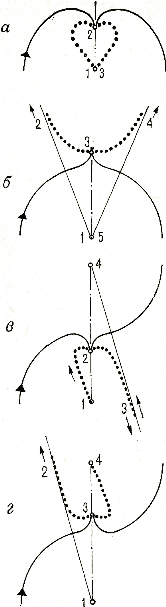 Рис. 14. Центроиды движения конька: а — тройка; б — скобка; в — крюк; г — выкрюк
Поскольку в выкрюке наиболее сложный участок (смена направления скольжения) расположен до поворота, а не после, как в крюке, поэтому фигурист проходит его почти в статическом положении. В результате выкрюк выполнять, как правило, легче, чем крюк, где смена направления скольжения происходит после поворота, на фоне сложного движения разрешения, после которого точность скольжения затруднена.
Наиболее сложная форма центроиды в повороте скобкой. Здесь центроида имеет два разрыва — до и после поворота. Особенно трудно изменение направления скольжения конька после поворота, где, как и в крюке, точность скольжения осложнена последствиями движения разрешения. Следует учитывать, что приведенные центроиды соответствуют движению конька, а не всего тела. Именно поэтому нельзя ставить знак равенства между вращениями конька и вращением всего тела.
Итак, можно сделать следующие выводы.
1. При выполнении обязательных фигур телу фигуриста не должно сообщаться общее вращение вокруг его продольной оси.
2. Механизм вращательного компонента поворотов заключается во встречном вращении верхней части тела относительно нижней. При этом кинетический момент нижней части тела равен по величине и противоположен по знаку кинетическому моменту верхней части тела и кинетическому моменту потерь.
3. Показателем результирующего вращения частей тела является движение конька. Для точного соблюдения геометрической правильности кругов опорный конек фигуриста должен поворачиваться вокруг оси мгновенного вращения, проходящей через центр круга.
Правильная форма поворотов может быть соблюдена, если при их выполнении опорный конек в каждый момент поворачивается вокруг оси мгновенного вращения, последовательно перемещающейся по эталонной центроиде этого поворота.
4. Сложность выполнения поворота связана с конфигурацией центроиды движения конька в этом повороте.
ОТТАЛКИВАНИЕ
При выполнении больших фигур, таких, например, как параграф, фигурист совершает путь длиной около 170 м (9 кругов радиусом 3 м). На этом пути он делает 6 отталкиваний, после каждого отталкивания проезжая около 28 м. Естественно, что, отталкивания, выполняемые для приобретения нужной скорости, играют важную роль при выполнении фигуры.
Перед отталкиванием фигурист сгибает обе ноги, делая упор на толчковую ногу. Сумма углов в суставах (коленном и голеностопном) каждой ноги в большинстве случаев одинакова. Разгибая толчковую ногу, спортсмен сообщает начальную скорость опорной ноге, которая начинает сгибаться и сгибается до того момента, пока толчковая нога окончательно не выпрямится. Затем опорную ногу разгибают до положения свободного скольжения, и дальше движение идет на опорной ноге по инерции.
Изменения углов в суставах опорной и толчковой ног, подсчитанные у группы девушек-фигуристок, приведены в таблице.
Как видим, в процессе отталкивания сумма углов в суставах толчковой ноги увеличилась на 83° (270°— 187°), а сумма углов в суставах опорной ноги уменьшилась на 15° (187°—172°), причем изменение произошло в основном за счет коленного сустава, угол в голеностопном суставе изменился мало.

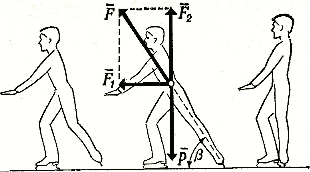 Рис. 15. Составляющие силы отталкивания
Фигурист получает начальную скорость, необходимую для выполнения обязательной фигуры, благодаря разгибанию толчковой ноги. Образующаяся при этом сила направлена вдоль прямой, соединяющей о.ц.т. с точкой касания конька толчковой ноги со льдом в конце отталкивания. Угол р, образованный силой отталкивания с ее проекцией на плоскость льда, назовем углом отталкивания.
На рис. 15 видно, что силу отталкивания F можно разложить на две составляющие F{ и F2, из которых F2 уравновешивается силой веса Р, a F\ приводит фигуриста в движение. Таким образом, не вся сила отталкивания используется для сообщения фигуристу начальной скорости, а только одна из ее составляющих F\. Обе они связаны соотношением /7! = /?-cosp, где р— угол оттал* кивания.
Для определения величины силы отталкивания можно использовать известную в механике зависимость, которую для нашего случая можно записать в следующем виде: mv = Fi-t, где т — масса тела; v — скорость в конце отталкивания; F\—горизонтальная составляющая силы отталкивания; t — время отталкивания.
Дело в том, что, приобретая нужную начальную скорость, фигурист может варьировать силу отталкивания в зависимости от его времени.
Допустим, фигуристка весит 47,7 кг; для выполнения фигуры нужно иметь начальную скорость и = 2,4 м/сек. Если отталкиваться в течение 0,3 сек., необходима, сила а если отталкивание продолжается 0,5 сек., то для получения скорости и = 2,4 м/сек достаточно силы 23,5 кг. Для данного веса фигуристки и заданной начальной скорости можно построить график изменения силы Fi в зависимости от времени отталкивания / (рис. 16).

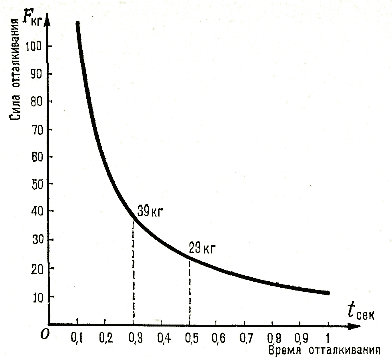 Рис. 16. Связь начальной скорости с силой и временем отталкивания
| 
